ホーム > 県政情報・統計 > 統計情報 > 統計情報総合案内 > 統計情報の広場(千葉県の統計情報) > 分野別検索 > 総合 > 指標で知る千葉県 > 指標で知る千葉県2001 > 指標で知る千葉県2001・利用上の注意

指標で知る千葉県2001・利用上の注意

千葉県企画部統計課
電話043-223-2217
FAX043-227-4458

1.　項目名に（人口〇〇当たり）とあるもので特に断り書きのない場合は、都道府県編では総務省統計局公表の当該年10月1日現在推計人口（国勢調査年については国勢調査人口）を使用し、市町村編では千葉県企画部統計課公表の当該年10月1日現在常住人口（国勢調査年については国勢調査人口）を使用している。

2.　時点の「○○年」は暦年（1月～12月）、「○○年度」は会計年度（4月～翌年3月）を示している。

3.　表中データ値は、原則として単位未満を四捨五入してある。このため、各データの合計が総数と一致しない場合がある。

4.　記号の用法等は、次のとおりである。

• 「＊」　推計値、または、暫定値
• 「0」　データが「0」、または、単位未満のもの
• 「-」　データが無い、または、「指標計算式」の分母データが「0」のもの

5.　都道府県編は、データ値の高い順に都道府県を配列している。また、同順位の場合は、都道府県コード順に配列している。

市町村編は、平成12年4月1日現在市町村コード順に配列している。

6.　平均値、標準偏差及び偏差値について

i.　データ全体のばらつき具合等の特徴（○○から○○の範囲に広がっている等）や個別データの特徴（平均よりどのくらい上なのか下なのか等）を数値で表したものが平均値、標準偏差及び偏差値である。

ii.　算出方法

（データ全体を代表する値）

（データ全体のばらつき具合を表す値）

（平均値を「50」と表した場合、データ全体のばらつき具合から個別データの全体から見た位置を表す値 ）

iii.　標準偏差

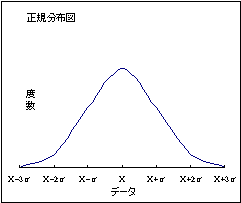
データ集団をいくつかの級に分けた級ごとのデータ数を「度数」とよび、データと度数を対応させた図を「度数分布図」とよぶ。
このデータ集団が右図のように平均値を中心に左右対称でつり鐘型となる分布状態を「正規分布」とよび、この図を「正規分布図」とよぶ。

正規分布であるデータ集団と平均値、標準偏差との間には、次の関係が成立している。

• (1)　X±σの範囲に全データの68.3％がはいっている
• (2)　X±2σの範囲に全データの95.5％がはいっている
• (3)　X±3σの範囲に全データの99.7％がはいっている

よって、σが大きければ広がりの幅は広くなり、σが小さければ広がりの幅は狭くなる。このことから、標準偏差σによって、データ集団がばらつきの大きい集団なのか、ばらつきの小さい集団なのかがわかる。

iv.　偏差値

上記のように、データ集団のばらつき具合は様々であるため、実数データからだけでは、あるデータが集団の中でどの位置にいるのかわかりにくい。

このため、平均値を一律「50」とし、ばらつき（つまり標準偏差）を標準化して個々データの値を算出したものが「偏差値」である。

〈例〉

下記のようなデータ集団A、Bがあり、平均値はXA＝XB＝70と等しい。
A：60,65,65,70,70,70,70,75,75,80
B：40,50,60,65,70,70,75,80,90,100
ここで、それぞれの集団の標準偏差を算出すると、
σA　≒　5.5、 σB　≒　16.9
となる。

このことから、集団A、Bは平均値は同じであってもばらつき具合に大きな違いがあり、集団Aはばらつきが小さく、集団Bはばらつきが大きいため、このままではデータ比較がしにくい。

そこで、集団Aにおけるデータ「 75 」と集団Bにおけるデ ー タ「 80 」の偏差値を算出すると、
偏差値（Aの75）≒　59.1、　偏差値（Bの80）≒　55.9
となる。

このことから、実数でみると「75」より「80」の方が高いが、集団全体の中での位置づけからみると、集団Aにおける「75」の方が集団Bにおける「80」より高いことがわかる。

都道府県編では、平均値として各都道府県データ値の単純平均値を用いている。（よって、全国値と平均値は一致しないため、千葉県データ値が全国値を上回る場合でも偏差値が50を下回る場合がある。）

また、数値のみから事の善し悪しをいちがいに判断することは適当ではないため、ここでは一律にデータ値の高いものが偏差値が高くなるように算出している。
なお、市町村編では、平均値及び標準偏差のみ算出している。

7.　問い合わせ先

千葉県企画部統計課統計情報班　（TEL　043-223-2217）